
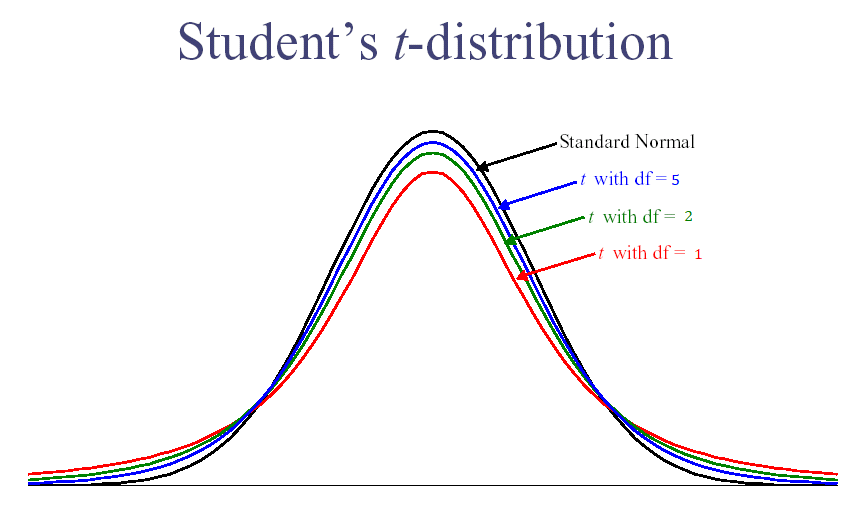
The use of the t-distribution arises when performing hypothesis testing (for the case when the population standard deviation is not known). We can either use specialized software such as Excel, etc, or we can use t-distribution tables (normally available at college statistics textbooks.
For a more interactive t-table, along with the t-distribution, follow the Excel template in Figure 2.3. 05 probability that a sample will have a t-score > 2.015. The t-distribution "converges" to the standard normal distribution as the number of degrees of freedom (df) converges to infinity (\(+\infty\)), in the sense that its shapes resembles more and more that of the standard normal distribution when the number of degrees of freedom becomes larger and larger.Ĭompute probabilities associated to the t-distribution In Table 2.2, a sampling of a student’s t-table, it shows the probability of exceeding the value in the body. For one sample, the number of degrees of freedom is df = n - 1, where n is the sample size It is determined by one parameter: the number of degrees of freedom (df). It is "bell shaped", in the same way the normal curves are bell-shaped It is continuous (and as a consequence, the probability of getting any single, specific outcome is zero) The main properties of the t-distribution are: The t-distribution is a type of continuous probability distribution that takes random values on the whole real line. x is the value at which the distribution is. Here 2 F 1 is the hypergeometric function. Let's understand the cumulative distribution function for the t distribution with different degrees of freedom. The T distribution function varies with degrees of freedom.
This is calculator for the T-Distribution.More About this T-distribution Graph Maker T distribution is a bell shaped curve but much flatter than normal distribution curve. In order to compute probabilities associated to the t-distribution we can either use specialized software such as Excel, etc, or we can use t-distribution tables (normally available at college statistics textbooks. The t-distribution "converges" to the standard normal distribution as the number of degrees of freedom (df) converges to infinity (+∞)


 0 kommentar(er)
0 kommentar(er)
